Aanpassing (statistiek)
In de statistiek spreekt men van aanpassing als de parameter(s) geschat worden van de kansverdeling die zo goed mogelijk past bij een reeks waarnemingen. De mogelijke kansverdelingen behoren tot een geparametriseerde klasse en op basis van de waarnemingen wordt de parameter of worden de parameters geschat, waarbij verschillende criteria voor goed passen kunnen worden gehanteerd. Men zal een aangepaste verdeling bepalen als met deze verdeling meerdere kansuitspraken gedaan moeten worden.
In de hydrologie, bijvoorbeeld, is het van belang de kans op een hoge rivierafvoer die eens per zoveel jaar voorkomt, te voorspellen. Hiervoor kan een aangepaste kansverdeling worden gebruikt en toegepast bij het ontwerp van verdedigingswerken tegen overstroming.[1]
Mogelijke verdelingen
[bewerken | brontekst bewerken]
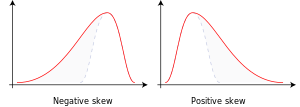
Er zijn veel verschillende klassen van kansverdelingen waaruit kan worden gekozen. Onderscheid kan worden gemaakt in symmetrische en scheve verdelingen.
Symmetrische verdelingen
[bewerken | brontekst bewerken]Als de gegevens symmetrisch (spiegelbeeldig) rond het gemiddelde zijn verdeeld, waarbij het aantal malen van voorkomen (de frequentie) afneemt met de afstand tot het gemiddelde, kan men bijvoorbeeld de normale verdeling, de 'logisitieke verdeling', of de Studentverdeling toepassen. De eerste twee komen sterk overeen terwijl de laatste, met 1 vrijheidsgraad 'dikkere staarten' heeft, maar ook een hogere, hoewel dunne piek (de verdeling heeft bij dezelfde spreidingsmaat een hogere kurtosis).
Scheve verdelingen
[bewerken | brontekst bewerken]Als de grotere waarden verder verwijderd zijn van het gemiddelde dan de kleinere, is de verdeling 'scheef' naar rechts (er is positieve scheefheid). In dat geval kan men een keuze maken uit de lognormale verdeling (dat wil zeggen dat de logaritmen van de waargenomen waarden normaal verdeeld zijn), de 'loglogistieke verdeling', de 'Gumbel-verdeling', de exponentiële verdeling, de 'Fréchet-verdeling', de Pareto-verdeling, of de Weibull-verdeling. Enkele van deze verdelingen zijn 'links begrensd', of wel: waarden beneden deze grens kunnen niet voorkomen.
Als de kleinere waarden verder verwijderd zijn van het gemiddelde dan de grotere dan, is de verdeling scheef naar links (er is negatieve scheefheid). In dat geval kan men een keuze maken uit de 'wortelnormale verdeling' (dat wil zeggen dat de wortels van de waargenomen waarden normaal verdeeld zijn) en de 'gespiegelde Gumbel-verdeling'. Enkele van deze verdelingen zijn 'rechts begrensd', of wel: waarden boven deze grens kunnen niet voorkomen.
Aanpassingsmethoden
[bewerken | brontekst bewerken]De volgende manieren van aanpassing kunnen worden gebruikt: :[2]
- Momentenmethode
- Methode van L-momenten[3]
- Methode van de grootste aannemelijkheid[4]
Statistische betrouwbaarheid
[bewerken | brontekst bewerken]Een aangepaste kansverdeling zal in het algemeen in meer of mindere mate afwijken van de werkelijke verdeling. Ook kunnen toekomstige gebeurtenissen een andere verdeling hebben dan de verdeling waaruit de waarnemingen kwamen.
Externe links
[bewerken | brontekst bewerken]- Software voor het maken van aangepaste kansverdelingen
Referenties
[bewerken | brontekst bewerken]- ↑ E.H.Chbab en J.M. van Noortwijk (2002), Bayesiaanse statistiek voor de analyse van extreme waarden, RIZA Rijksinstituut voor Integraal Zoetwaterbeheer en Afvalwaterbehandeling, Lelystad. ISBN 9036954231. Online : [1]
- ↑ Frequency and Regression Analysis. Chapter 6 in: H.P.Ritzema (ed., 1994), Drainage Principles and Applications, Publ. 16, pp. 175–224, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. ISBN 9070754339. Free download from the from webpage [2] under nr. 12, or directly as PDF : [3]. Gearchiveerd op 7 november 2021.
- ↑ Hosking, J.R.M. (1990). L-moments: analysis and estimation of distributions using linear combinations of order statistics. Journal of the Royal Statistical Society, Series B 52: 105–124.
- ↑ Aldrich, John (1997). R. A. Fisher and the making of maximum likelihood 1912–1922. Statistical Science 12 (3): 162–176. DOI: 10.1214/ss/1030037906.
